Mikhail Naganov

Re-creating Phonitor Mini with Software DSP

If you have seen my previous posts, you might remember that my plan was to recreate Phonitor Mini crossfeed within miniDSP HA-DSP. However, while trying to do that I’ve encountered several technical difficulties. I would like to explain them first.

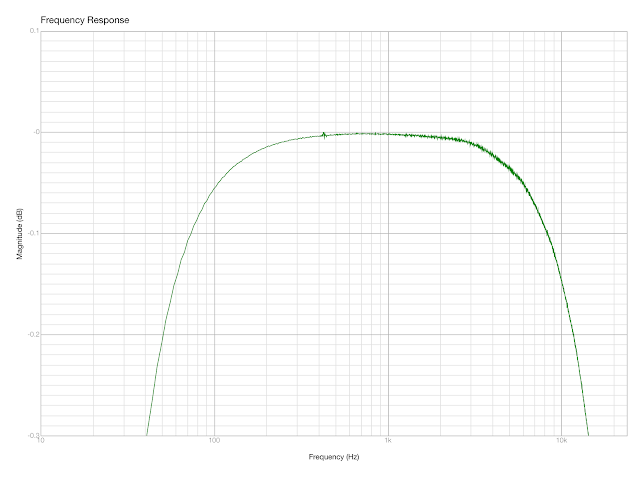
First, the hardware of HA-DSP looks good on paper, but flaws in the implementation can be easily detected even using an inexpensive MOTU Microbook IIc. For starters—look, there is some noise:

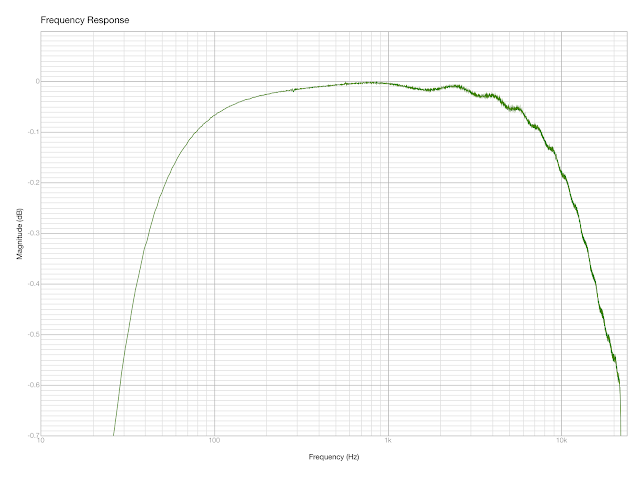
Yes, it’s at microscopic level, but I don’t see anything like that on MOTU cards, that also employ DSP. And the resampler (recall that the DSP in HA-DSP operates at 96 kHz) adds some wiggles when working with 48 kHz signals:

Finally, I’ve experienced stability issues when connecting HA-DSP to Android and Linux hosts. I raised the last two issues with miniDSP support, but got no resolution.

Another technical problem came from FIR filter design software. I use FIRdesigner, and it’s quite powerful and versatile tool. However, it has one serious drawback in the context of my scenario—since the Phonitor crossfeed filters are quite delicate, and have only a 3 dB amplitude at most, when modeling them, every fraction of a decibel counts. But since FIRdesigner is first and foremost designed for speakers builders, it only offers 0.1 dB precision when manipulating the source signals, and that was causing non-negligible deviations of the designed FIR filters’ frequency response curve when compared to the original curves of the analog Phonitor filters.

I’ve been wrestling with these issues for a while, then thought the situation over, and decided to sell my HA-DSP. Having parted with it, I turned back to my initial approach of performing filtering in software.

There had been some work already done by myself for generating IIR filter coefficients to fit a given frequency response using cepstral method (based on this post by R. G. Lyons). So I have dusted off my Matlab / Octave code, and prepared it for action.

However, one important thing had to be done to the analog filter measurements—since I was performing them using MOTU Microbook IIc which lacks ideally flat frequency response, I needed to remove frequency response roll-offs introduced by it from these measurements. On the DSP language this process is called deconvolution—”reversing” application of a filter.

I’ve learned that it’s quite easy to perform deconvolution with REW, although the command is buried deep in the UI. Big thanks to REW’s author John Mulcahy for pointing this out to me!

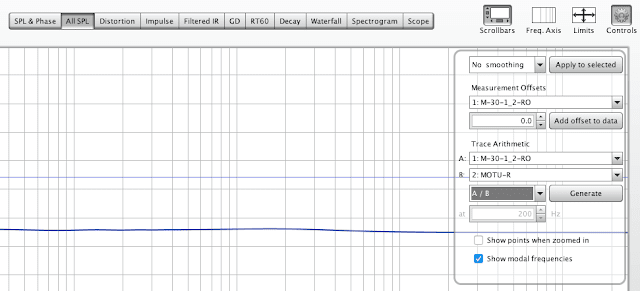
In order to perform deconvolution in REW, two measurements first need to be imported. In our case the first measurement is the Phonitor’s filter curve recorded via Microbook, and the second one is a loopback measurement of Microbook on the same output and input ports. Then, on the All SPL tab one need to open the drop down menu (the cog button), select these measurements, and choose division (/) operation. Division in the frequency domain is equivalent to deconvolution performed in the time domain.

One important thing to remember is to always save all impulse responses with 32-bit resolution because quantization errors can cause quite visible deviations of the calculated frequency responses.

Now, having nice deconvolved impulse responses, I was ready for action. Since this time I was creating a software implementation of a filter, I’ve got more freedom in choosing its parameters—no more was I constrainted by the sampling rate of the DSP or the number of taps on it. So I’ve chosen to create an IIR filter operating at 44.1 kHz sampling rate, and having 24th order.

The resulting model has turned out to be ideally close to the target filter. Note that on the plot, the offset of the curves for the direct and the opposite channels isn’t correct—this is because during deconvolution, the amplitudes of the filters were normalized by REW. Never mind, it’s easy to fix.

In order to figure out what is the offset between the direct and the opposite channel filters, I used a nice feature of FuzzMeasure’s interactive plots—after clicking a point with “Option” key pressed, FM shows both the variable value (frequency in this case), and the corresponding values of the displayed graph, with precision of 3 digits after the decimal point. So it was quite easy to find out what is the difference between the filter curves for the direct and the opposite channels.

Using this information, I was able to fix the offset of my curves, and finally was ready to process some real audio. I’ve chosen a short excerpt form Roger Waters’ “Amused to Death” album, where a lot of different kinds of sounds present: male and female vocals, bass, percussion, guitars, etc. The recording quality is outstanding, plus the final result was rendered using QSound technology which uses binaural cues for extending the stereo base when listening on stereo speakers. It’s interesting that when listening on headphones without crossfeed, all these cues do not work due to “super stereo” effect. But they start working again with crossfeed applied.

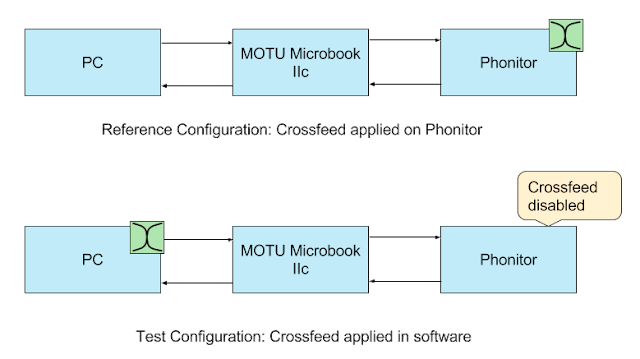
For blind tests, I’ve passed a fragment of “Perfect Sense, Pt. II” song through a rig of Phonitor Mini connected via Microbook. First in its original form, but with Phonitor’s crossfeed applied, and then after processing via the IIR filter I have created, with crossfeed on Phonitor turned off. This way, the difference between these recordings were only in the implementation of the crossfeed effect.

Below are the links to the original recording, the one processed with Phonitor’s own crossfeed, and with my digital re-implementation of it (make sure to listen in headphones):

Original | Phonitor crossfeed | IIR implementation

In my blind test, I couldn’t distinguish between the original crossfeed and my model of it (two last samples).

Then I wanted to try to process a couple of full length albums. Here I’ve got a little problem—the way sound processing is organized by default in Matlab and Octave doesn’t really scale. There is a function called audioread for reading a portion of audio file into memory in uncompressed form (and there must be a continuous region in memory available for allocating the matrix that contains the wave samples). And there is a complementing function called audiowrite which writes the result back to disk. However, it would require creating custom code in order to read the input file in fragments, process it using the filter and write back.

I decided to do something different. Since I anyway was planning applying a headphone normalization filter in Audacity, I though it would be convenient to perform crossfeed processing in Audacity as well.

There is an entire scripting language in Audacity hidden behind Effects > Nyquist Prompt… menu item. The script “sees” the whole input wave as a single object, but behind the scenes Audacity feeds to the script bite-sized chunks of the input file. That’s the abstraction I wanted. So I wrote a Matlab script that transforms my high-order IIR filter into a sequence of biquads, and generates a Nyquist Prompt script that performs equivalent processing.

Since biquad filters are implemented in Nyquist Prompt in native code, even a sequence of 12 biquads gets applied quite quickly, and the entire CD is processed on my modest Mac Mini 2014 in slightly more than a minute. The generated Nyquist Prompt script is here. Note that it is needed to enable “Use legacy (version 3) syntax” to work with Lisp code.

One caveat was to avoid losing precision while applying the sequence of filters. My initial mistake was to export the biquad coefficients with just 6 digits after the decimal point—the processed file was sounding awful. Then I enhanced precision, and diffed the sound wave processed in Audacity with the same wave processed in Octave. The diff wave only contained some noise below -100 dBFS, and the two processed audio samples were now indistinguishable in a blind test.

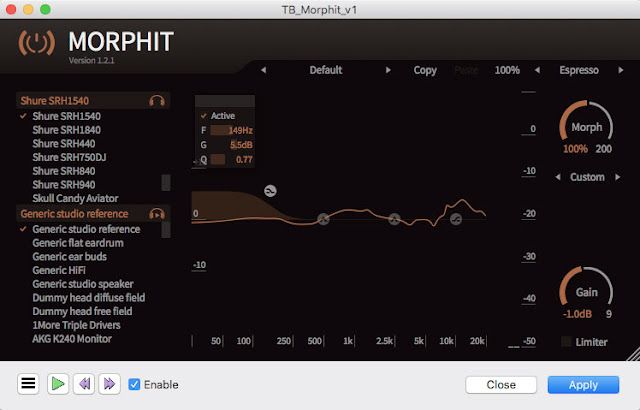
I have mentioned headphone linearization before. With ToneBoosters Morphit performing linearization is straightforward assuming that measurements of your headphones are in Morphit’s database. My first impressions after listening to processed audio samples was that Morphit thins out bass considerably. I’ve compared Morphit’s equalization curves with Harman’s Listener Target Curve for headphones and found that the former lacks the bump in the bass area featured in the latter.

So I’ve switched to custom mode in Morphit, and compensated the applied shaving off of the bass with a shelf filter:

The resulting audio sample sounded much better both than the original version processed with the crossfeed filter (due to more prominent vocals and percussion), and definitely better than the initial linearization by the factory Morphit filter for Shure SRH1540.

By the end of the day, I’ve created processed wavefiles of some quality recorded albums I have on CDs, and uploaded them into my Play Music locker for further evaluation. I didn’t notice any harm from the compression to 320 kbps. Now, would I enjoy this crossfeed+Morphit processing on the albums I know well, I will find a way to apply the processing in real time to all sound output on my Linux workstation.